熱通過率ってなんなの?総括熱伝達率とか熱貫流率とか、名前もなにがなんだかわからない上に、どんなものかもわからない。とにかく数字を使わず、イメージで教えてほしいわ。
こんな悩みにお答えします。
まず先に言っておくと、熱通過率・総括熱伝達率・熱貫流率、この3つは全て同じ意味です。なので覚えることは一つなので安心してください。
そして、熱伝導率、熱伝達率を勉強すると、最後のボスとして熱通過率という言葉がでてきます。
熱伝導、熱伝達、熱通過、これはいわば三兄弟のようなものですね。
最後に出てくる一番強い三男的なポジションですので、ぜひ覚えるようにしましょう。
今回の内容はこちら!
- 熱通過率について
- 熱伝達率・熱伝導率との違い
- 熱通過率の計算式
最後は計算式でどのようになっているかを示しますが、最初はイメージでわかりやすく解説しているので安心してください。
ちなみに、熱伝導率、熱伝達率については以下の記事をご覧ください。
もくじ
熱をはじからはじへ伝える度合いが熱通過率
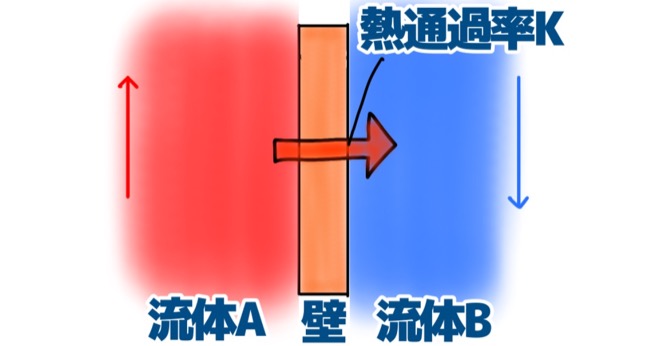
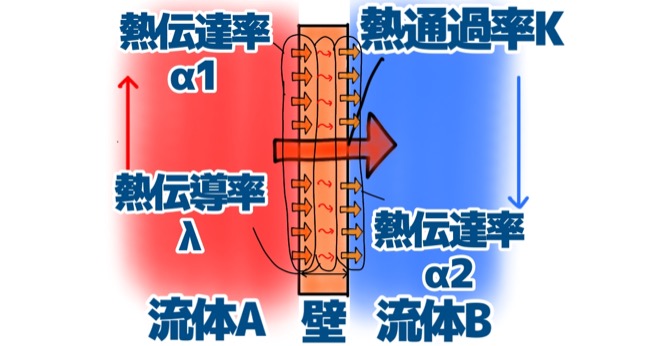
熱通過率というのは、壁で隔てられた流体Aと流体Bにおいて、熱がどんな割合で伝わっていくかを表したものです。
上の絵を例にとって考えます。
熱い流体Aと、冷たい流体Bが、互いに壁で隔てられて流れているとします。
流体Aは下から上へ、流体Bは上から下へ流れているとします。
流体Aは高温、流体Bは低温だとすると、熱はあついところから冷たいところに移動するので、熱の流れはA→Bとなります。
この時、AからBへ移動した熱の割合を、熱通過率と言います。
なんだか、熱伝達率と同じなんじゃないか、と思うかもしれませんが、少し違います。
ここからその違いについて説明していきます。
流体Aから流体Bまでの熱の伝わり順を考える
熱が流体Aから流体Bまで伝わっていくとき、いきなりAからBに伝わることはありません。
AからBへ熱が伝わっていくには、3つの段階を踏んでじわじわと熱が伝わっていきます。
以下ではその3ステップを解説します。
流体Aから壁に熱を伝えるのが熱伝達率
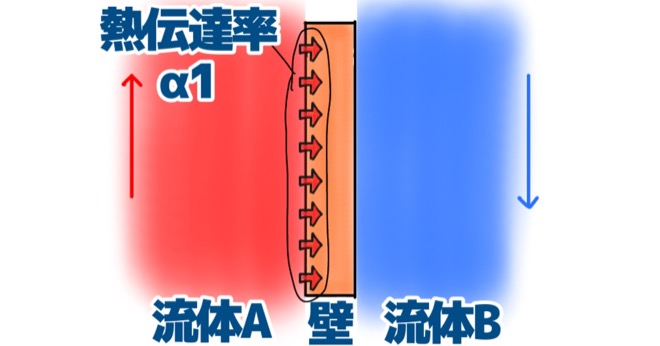
まず、流体Aがもつ熱は、壁に伝わりますね。
これは、熱は流体Aから壁へと、違う物質へ伝わっていますので、熱伝達率で表すことができます。
壁に熱が行き渡るのが熱伝導
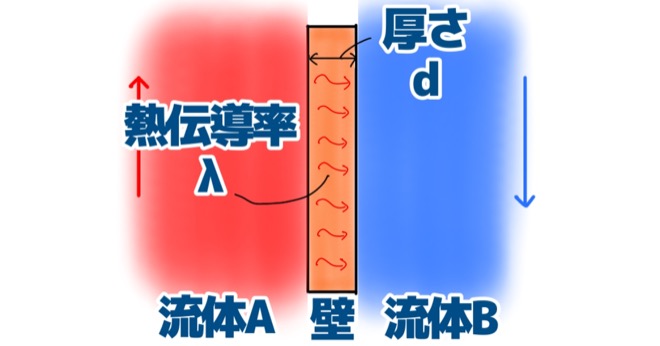
次に、壁に伝わった熱は、じわじわと右側へ伝わっていきます。
これは、一つの物質の間で熱を伝えているので、壁がもつ熱伝導率の大きさによって熱の伝わり具合が左右されます。
金属の壁なら熱伝導率が高いためすぐに熱は伝わり、逆に熱伝導率の低い壁はゆるやかに熱を伝えていきます。
壁が流体Bに熱を伝えるのが熱伝達率
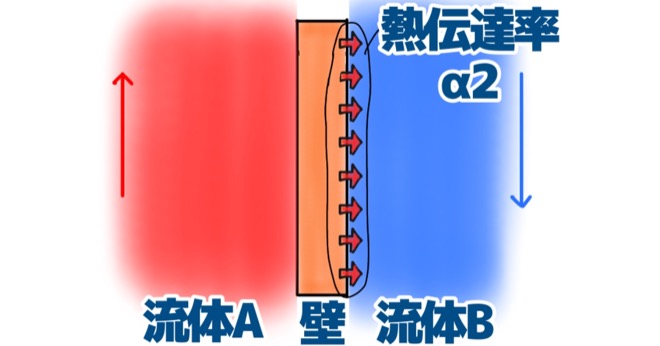
壁の端までたどりついた熱は、やっと流体Bをあたためることができます。
これは、流体Aが壁に熱を伝えるのと一緒で、違う物質へ熱を伝える現象なので、熱伝達率で表します。
これが流体Aから流体Bに熱を伝える全プロセスになります。
このようにして熱は伝わっていくんですね。
熱の伝わりを全部足したものが熱通過率
さて、今まで3つの熱の伝わりを見てきましたが、これらの熱の伝わり方を全て足したものが熱通過率というものになります。
つまり、1つの熱伝導現象、2つの熱伝達現象ですね。
これらを全部足し合わせたものが熱通過率として表されるんです。
熱通過率を計算式
それではここから、実際にどのように計算されるかを示していきます。
さきほどから使っている絵を例にとり、下のように定義します。
-
\( \alpha _{1} \):流体Aが壁へ熱を伝えるときの熱伝達率 \\
\( \alpha_{2} \):壁が流体Bへ熱を伝えるときの熱伝達率
\( d \) :壁の厚さ
\( \rho \) :壁の熱伝導率
\( K \):熱通過率
すると、流体Aから流体Bへの熱の流れかたを示す熱通過率は、次の式のように表すことができます。
$$\frac{1}{K} = \frac{1}{\alpha_{1}} + \frac{d}{\rho} + \frac{1}{\alpha_{2}} \tag{1}$$
流体Aと壁の組み合わせで熱伝達率が変われば、熱通過率も変わるし、壁の厚みが厚ければ、当然熱通過率も変わってきますね。
生活でもイメージできますが、部屋をあったかくしたいとき、薄い壁と厚い壁、どちらがいいですかと聞かれれば、当然厚い壁ですよね。
寒い日に、厚着でいるのと薄着でいるの、どちらが暖かいですかと聞かれれば、当然厚着でいるほうがいいですよね。
熱の伝わりは壁の厚さにも関係するんですね。
最後に
このように、流体Aから流体Bに熱を伝えるには、3つの熱移動現象が関係し、それを表す熱通過率の式は、2つの熱伝達率と、1つの熱伝導率、それと壁の厚さで表せることがわかりました。
熱伝達率と熱伝導率を組み合わせたものが、熱通過率となって計算できるようになる、ということですね。
今回は以上です。

