圧力容器の応力【薄肉円筒胴の計算方法】図12枚でやさしく解説

冷凍機械の試験では、圧力容器が必ず出題されます。

難易度は一冷が圧倒的ですが、二冷、三冷でも圧力容器の問題は必ず出題されています。

結論から言うと、薄肉円筒胴の応力のポイントとしては、以下のように書くことができます。

特に接線方向の応力\(\sigma_t\)は長手方向の2倍である、という問題は三冷でも出題されますので覚えておくようにしましょう。

今回は薄肉円筒胴における接線方向、長手方向の応力の公式を、イメージでわかりやすく、絵をたくさん使いながら解説していきます。

薄肉円筒胴について

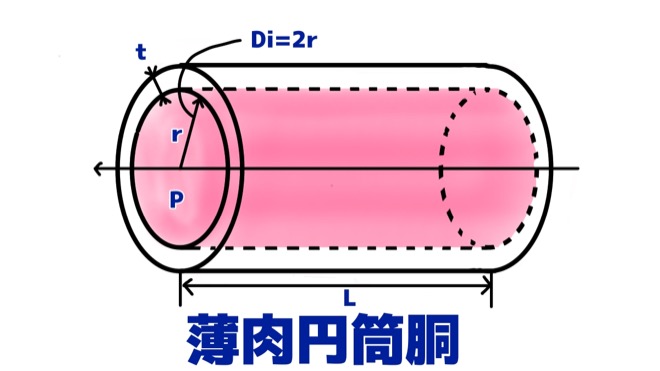
圧力容器の中で、薄肉円筒胴はよく使われる形状です。

ドラえもんのアニメの中で、のび太たちが集まる空き地の真ん中に３つある、土管のような形状をしています。

通常はその両端に皿型鏡板のようなものを溶接して、圧力容器としています。

シェルアンドチューブ凝縮器などはまさにこの形をしています。

また、“薄肉”とは、板の厚みのことです。

厚さが円筒胴の長手方向に対して非常に薄いため、薄肉と呼ばれます。

ここで、円筒胴の厚さをt、円筒胴の内径をDi、長手方向の長さをＬとします。

円筒胴のどの方向にどのような応力がかかるかを計算していきます。

応力

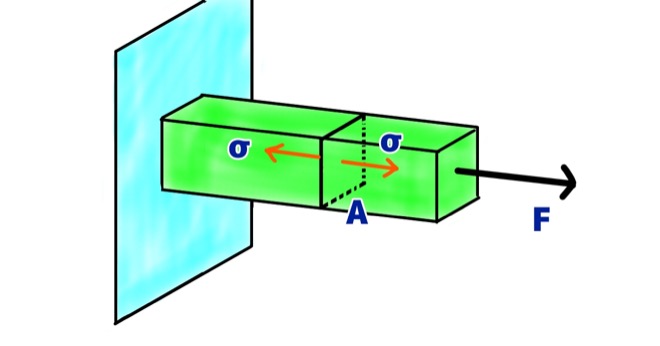
応力についての復習です。

応力σは、材料の内部に発生する力F[N]を、作用している面積A \( \rm[m^2]\)で割ることによって求めることができます。

$$ \rm{\sigma＝\frac{F}{A}}{\tag{1}}$$

ここで応力の単位は圧力と同じ[\( \rm N/m^2\)]ですが、応力は材料の内部に発生する単位面積あたりの力であることに注意してください。

応力の方向

上で定義した薄肉円筒胴の内部に、圧力Pの気体が封入されていたとします。

このとき、円筒胴にはどの方向に応力がはたらくかを考えます。

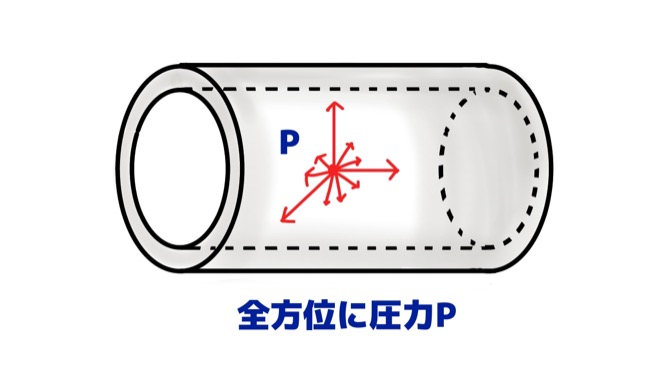
気体の圧力Pは、上のような点を基準に考えると、その点を中心に全方位に働いています。

これでは複雑なので、考えるべき圧力の方向を限定します。

すると、この方向は二つの基準の方向で表すことができます。

それが、接線方向と長手方向です。

他のどの方向に延びる圧力のベクトルを選んでも、全ての圧力は接線方向と長手方向に分解できます。

ですので、薄肉円筒胴に働く応力について考えるときは、接線方向にかかる圧力と、長手方向にかかる圧力について考えればよいことになります。

接線方向にはたらく応力

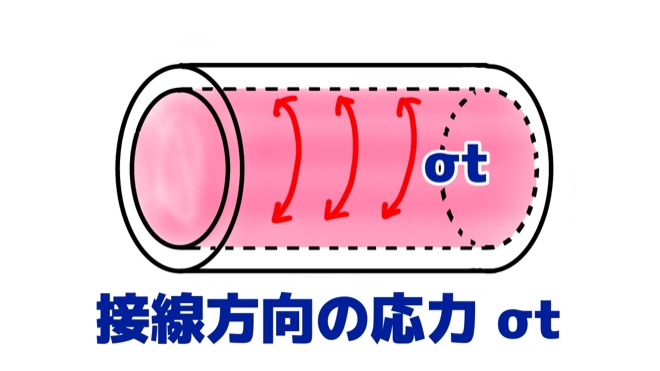
接線方向にかかる応力σtについて考えます。

接線方向と記述する場合もあれば、円周方向と書いている教科書もあるので注意してください。

結論から言うと、接線方向にかかる応力σtは以下の式で表されます。

以下ではこの応力σtの導出方法について解説していきます。

接線方向の応力の導出方法

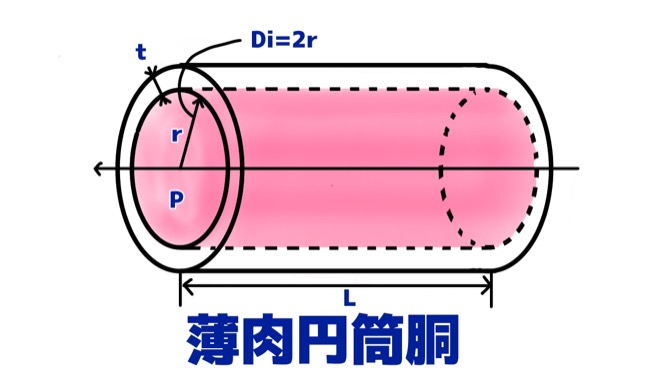
まず、復習として薄肉円筒胴を図1のように定義します。

ここで、円筒胴の内側直径はDi、板厚はt、それが長さLとして、内部には圧力Ｐが加わっているとします。

ここからは以下の順番で考えていきます。

道筋を知ってから読んでいった方が、どこへ向かっているのかわかるので理解しやすいと思います。

それでは順にみていきましょう。

ステップ１　円筒胴を半分に切って考える

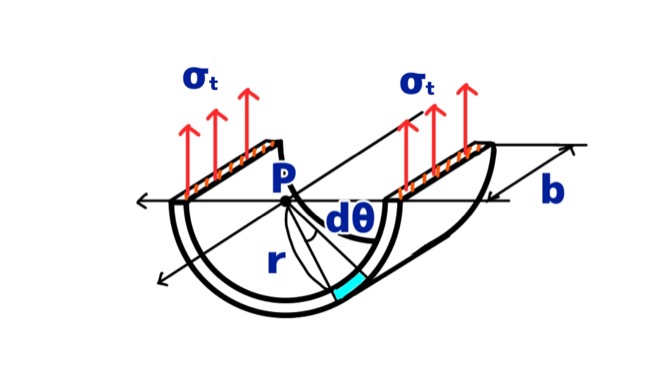
円筒胴を、図6のように水平に半分に切って考えてみます。

すると、接線方向の応力σtは円筒胴の切り口にかかっています。

また、応力がかかる切り口の面積は、板厚tと長さbなのでtbですが、両側にかかるので全体としては2tbですね。

ステップ２　円筒胴にかかる力Fを考える

応力の式は以下のように定義されると先ほど復習しました。

$$ \rm{\sigma＝\frac{F}{A}}{\tag{1}}$$

円筒胴にかかる応力はσtなので、かかっている力Fはいくつかというと、

応力に面積をかければよいので

$$ \rm{F＝\sigma_t \times 2tb=2tb \sigma_t } {\tag{3}}$$

これが円筒胴内にかかっている応力の力Fです。

ステップ３　圧力Pが与える力Ｗを考える

圧力Pが接線方向に作用するとき、その力Wを求めます。

このとき、少し特殊な考え方をしますが、中心からの微小角度ｄθと、長さbをかけたむらさき色の面積にかかる力dWを求めます。
あとでdWを円筒胴内の全体にわたって計算することで、力Wを求めていきます。

圧力Pは全体に一様にかかっているので、圧力Pに作用しているむらさき色の面積をかければdWを求めることができます。

この面積は、バームクーヘンの内側のところ、みたいなイメージですね。

むらさき色の面積は、rdθ×長さbでbrdθとなりますが、rdθの部分は、半径rの円の円周の計算は、半径×角度（ラジアン）で求めることができます。（円周の公式が2πrなのは、2π＝360°なので、そこにrをかけて円周を出している、と考えることができますね）

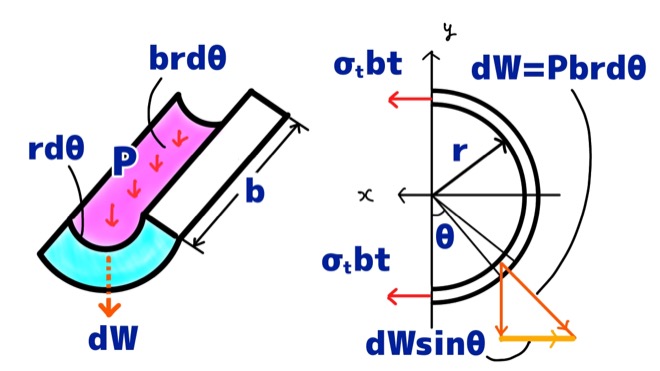
これを上から見てみると、この力dWは斜めの方向に働いています。

応力の力F＝σtbtはx方向なので、力のつり合いとするには、x方向についての力だけにする必要があります。

元の力dWはオレンジ色の方向にかかっているので、x方向にかかる力は角度θからdWsinθとすることができます（黄色の方向）

これを積分してx方向全体にかかる力Wを求めます。

θの範囲は

$$ { 0 \leqq \theta \leqq \pi }$$

なので、この範囲にわたって積分することで、x方向にかかる圧力の力Wを求めることができます。

すると、Wは次の式のようにかかれます。

$$ \rm{W＝\int_0^\pi dW \sin \theta }{\tag{4}}$$

dW=Pbrdθなので(4)式は

\begin{eqnarray}
W &=& \int_0^\pi \sin \theta Pbrd \theta \\
&=&Pbr\int_0^\pi \sin \theta d \theta \tag{5}
\end {eqnarray}

結局、Wは以下のようになります。年のため計算過程も詳しく書いておきます。

\begin{eqnarray}
W &=& Pbr\int_0^\pi \sin \theta d \theta \\
&=& Pbr \left[ -\cos \theta \right]_0^\pi \\
&=& Pbr (-\cos \pi + \cos 0) \\
&=& Pbr (1+1) \\
&=& 2Pbr \tag{6}
\end {eqnarray}


ステップ4　力のつり合いF＝Wを考える

ここまでくれば後は簡単です。先ほどの式より（2）式と（6）式の力のつり合いを考えると、

Ｆ＝Ｗより

$$ \rm{2tb \sigma_t = 2Pbr}{\tag{7}}$$

これより接線方向の応力σtは

となりました。

ここで、(8)式は半径rで表した場合、(9)式は直径Diで表した場合ですね。

このようにして、めでたく接線方向の応力を計算することができました。

続いて長手方向にかかる応力について計算していきます。

長手方向の計算の方が、接線方向の計算よりも簡単なので、すぐに終わらせられます。

長手方向に働く応力

次は長手方向にかかる応力σlを計算していきます。

こちらの方が計算手法としては簡単になりますが、やり方は同じです。

力のつり合いを見ていきましょう。

ステップ1　円筒胴をカットする

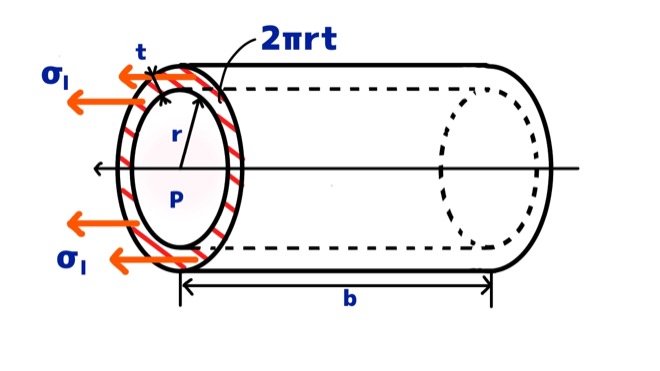
接線方向と同様に、円筒胴をカットして断面を見てみます。

といっても、これは最初から見ている方向と同じですね。

ステップ2円筒胴にかかる応力の力Fを考える

長手方向について考えているので、応力σlは円筒胴の左右方向にかかっています。

このときに力Fがどの面積にかかっているかというと、図9の斜線の部分全体です。

この面積は、円の内径の円周に板厚tをかけた2πrtとなります。

厳密に出す場合は外径の面積－内径の面積ですが、今回は薄肉でtがとても小さい、という前提ですので、このように計算して差し支えありません。

これより、長手方向の応力の力Fは次の式のようになります。

$$ \rm{ F = 2 \pi rt \sigma_l}\tag{10}$$

ステップ3　圧力Pが与える力Ｗを考える

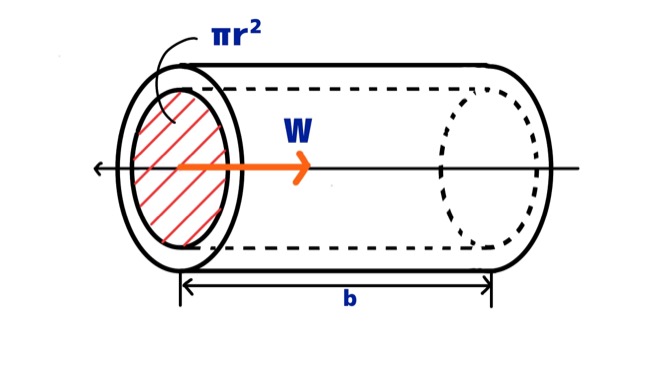
内部の圧力が与える力Ｗは図10のような方向になります。

すでに応力の力Fと方向が同じなので、接線方向のときのように力の方向を合わせる必要はありませんね。
力Wは、圧力Pに内径の面積\(\pi r^2\)をかけてあげればよいだけなので

$$ \rm{ W = P \pi r^2}\tag{11}$$

　

と簡単に描くことができます。

以上より、（10）式と（11）式の力のつり合いを考えれば

$$2 \pi rt \sigma_l = P \pi r^2 \tag{12}$$

となるので、結局以下のようになります。

と書くことができます。

応力の比較

上まででほとんど話は終わりですが、最後に覚えておくと得するポイントとしては接線方向と長手方向の応力値の大きさの違いです。

二つの応力の式はどちらも非常によく似ていて、これらの応力には下のような関係があります。

これはつまり、長手方向の応力値は、接線方向の半分だから、円筒胴の圧力容器の場合は接線方向のみ気をつけていれば問題ない、ということを意味しています。

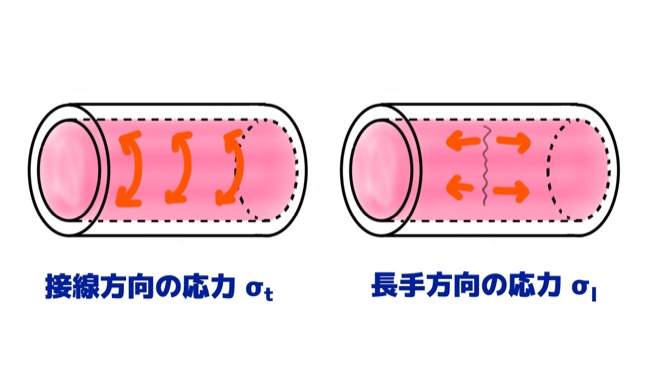
イメージで考えてみてもわかるかと思いますが、もしも円筒胴を破裂させようとした場合、接線方向のように全体が膨らむような力をかけるのと、円筒胴の両側を引っ張ってちぎれさせるような力をかけるのと、どちらが簡単に破裂させられるでしょう。

なんとなく引っ張ってちぎるのってたくさん力がいるって感じがしますよね。

実際計算でもそれを証明しており、き裂を生じさせるには、引っ張るよりも膨らませた方が簡単なんですね。

ですので、円筒胴の圧力容器の場合には、接線方向のみ気にしていれば問題ない、というわけです。

最後に

ここまで円筒胴の圧力用ににかかる応力を解説してきました。

3冷では式を用いたりすることは有りませんが、接線方向の応力は長手方向の2倍である、という問題は出題されます。

このあたり、イメージだけでもいいので覚えておくと得点につながります。

お役に立てば幸いです。