体積効率を求めるのに必要な計算式などが知りたいわ。でも、ただ数式を羅列しただけじゃ教科書と同じだから、式の意味も教えてほしいわ。
こんな悩みにお答えします。
今回は、体積効率の概念は理解しており、その上で体積効率を計算するのにどのような式を使用するかを解説する、いわば体積効率の上級編となります。
この記事に書かれていることを理解すれば、二冷はもちろん一冷の範囲でも通用する知識がつくと思います。
体積効率の基礎的な考え方は、下の記事で解説しましたので参考にしてください。
-

-
体積効率の意味・求め方【冷凍機械の圧縮機】イメージで解説|基礎編
三冷の範囲であればこれで十分だと思われます。
今回の内容はこちら!
- 体積効率の復習
- ピストン押しのけ量と吸込み蒸気量
- 冷媒循環量と吸込み蒸気量の関係
- 体積効率と圧力比(圧縮比)の関係
以下で詳しく、絵を用いてわかりやすく解説するので安心してください。
動画ではよりイメージしやすいように粘土を使って解説しているので参考にしてみてください。
体積効率の復習
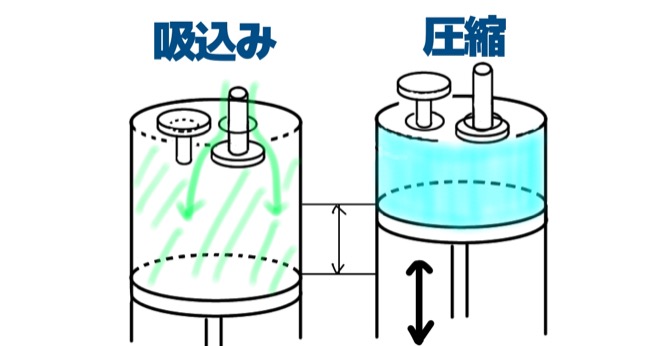
まずは体積効率に関して復習します。
体積効率\(\eta_v\)は以下のような式で描かれるものでした。
$$ \eta_{v}=\frac{q_{vr}}{V}\tag{1}$$
\(q_{vr}\):圧縮機の吸込み蒸気量
\(V\):ピストン押しのけ量
ピストン押しのけ量は、下の絵の通り、ピストンが動くことのできる黄緑色の範囲の体積でした。
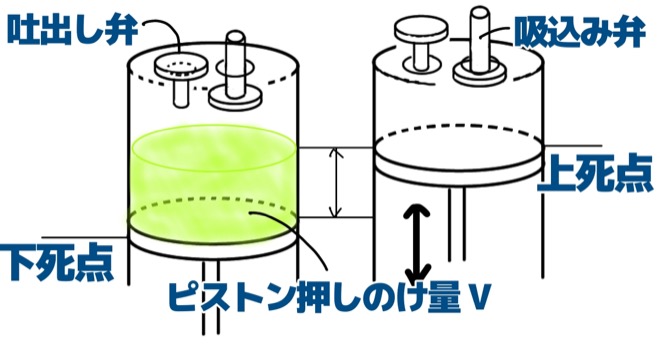
実際の吸込み蒸気量は、シリンダ内に冷媒が入り込むことができる量でした。
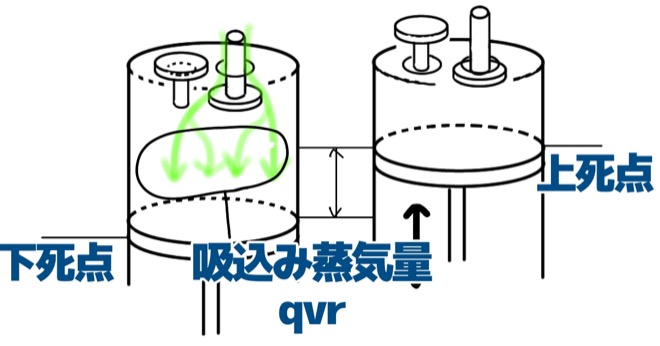
体積効率の肝心なところは、冷媒の吸込み蒸気量は、常にピストン押しのけ量よりも小さくなるため、体積効率が定義される、ということでした。
吸込み蒸気量がピストン押しのけ量よりも小さくなってしまう理由としては、以下がありました。
- トップクリアランス内の圧縮ガスの再膨張
- ピストン押しのけ量・吸込み蒸気量の数式解説
- 吸込み蒸気量と冷媒循環量の関係
これについて詳しく知りたい方は、最初に紹介した以下の記事で詳しく書いておりますので参照してください。

体積効率の意味・求め方【冷凍機械の圧縮機】イメージで解説|基礎編
ピストン押しのけ量
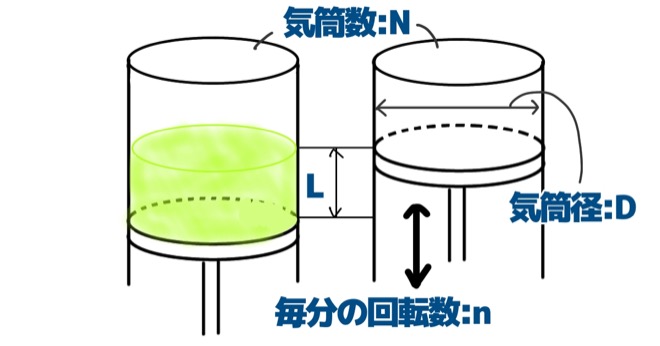
ピストンがどれだけ冷媒を押し込むことができるのか、押し込める体積を表したのがピストン押しのけ量でした。
もう少し専門的な用語で説明すると、1秒間あたりの冷媒ガスの理論排除容量のことで、ピストン行程容積(シリンダ容積)と回転速度によって決定され、以下の式で表されます。
ピストン押しのけ量
-
$$ V=\frac{\pi D^2}{4} \times L \times N \times \frac{n}{60} [m^3/s]$$
D:気筒径 [m]
L:ピストン行程 [m]
N:気筒数
n:毎分の回転数 [rpm]
ここで、\(\frac{\pi D^2}{4}\)とは、シリンダの面積のことです。
普通、円の面積は 半径×半径×πで表されますが、半径でなく、直径Dを用いて表す時は、上のように書かれるので注意しましょう。
(円の面積の式は、直径Dで表すと \( \frac{D}{2} \) × \( \frac{D}{2} \) × π なので、結局上の式になります)
機械系の学問ではこちらのように書くことも多いです。
単位は、単なる体積[\(m^{3}\)]ではなく、1秒間あたりの体積[\(m^3/s\)]であることに注意しましょう。
吸込み蒸気量

ピストン押しのけ量に対して、どれだけの冷媒を吸い込むことができるのか、それが吸込み蒸気量でした。
こちらも単位は1秒あたりにシリンダ内に吸込むことができる冷媒量なので、[\(m^3/s\)]になります。
この吸込み蒸気量が多いほど、体積効率は向上します。
吸込み蒸気量と冷媒循環量の関係
冷凍機の性能を表す時、冷媒循環量と比エンタルピーによって冷凍能力を計算しますが、この冷媒循環量は、吸込み蒸気量を用いて表すことができます。
冷媒循環量
-
$$ q_{mr} = \frac{q_{vr}}{v} = V \times \frac{\eta_v}{v} $$
\(q_{mr}\):冷媒循環量 [kg/s]
\(q_{vr}\):吸込み蒸気量 [\(m^3/s\)]
\(v\):比体積[\(m^3/kg\)]
\(V\):ピストン押しのけ量 [\(m^3/s\)]
\(\eta_v\):体積効率
単位を見てみるとこの式が正しいことがわかります。
冷媒循環量の単位は[\(kg/s\)]に対して、吸込み蒸気量は[\(m^3/s\)]です、体積[\(m^3\)]を[\(kg\)]に変換すれば、冷媒循環量[\(kg/s\)]の式に変えることができます。
ここで、比体積は密度[\(kg/m^3\)]の逆数なので、単位は[\(m^3/kg\)]ですね。
なので、吸込み蒸気量\(q_{vr}[m^3/s\)]を比体積\(v[m^3/kg]\)で割れば、単位が冷媒循環量の\([kg/s]\)になります。
もしも試験で冷媒循環量の導出方法を忘れてしまったら、単位をみると思い出しやすいと思います。
この辺り、もし良くわからない方がいたら、youtubeもやっていますので、気軽に質問してください。
圧力比(圧縮比)との関係

体積効率は圧力比と大きく関係があります。
圧力比とは、冷凍機の中での高圧圧力\(P_H\)と低圧圧力\(P_L\)の比です。
$$圧力比=\frac{高圧圧力}{低圧圧力} = \frac { P_H }{ P_L } $$
体積効率と圧力比には、下の図のような関係があり、圧力比が大きくなるほど、体積効率が低下していきます。
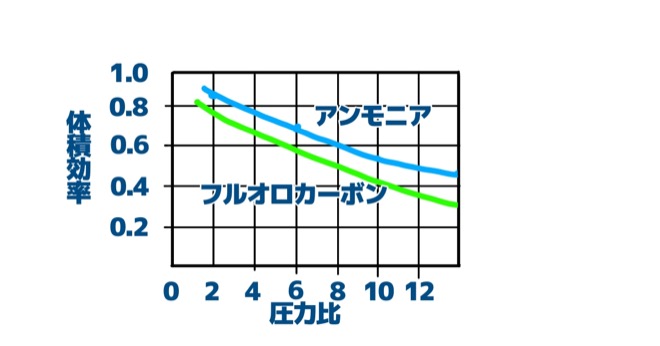
圧力比が大きくなると体積効率はなぜ低下していくのでしょうか。
圧力比が大きくなると体積効率が低下する理由
圧力比が大きいということは、圧縮機内のシリンダの内部と外部では、圧力差が大きくついています。
圧力差があると、冷媒漏れが大きくなります。このため体積効率は低下していきます。
この現象を、風船を膨らますことを例に考えてみます。
ほんの少しだけ空気を入れた風船の口から手を離しても、空気はそこまで勢いよく出ていきません。
ですが、空気をパンパンに入れた風船の口を離すと、ものすごい勢いで空気が出ていき、風船もロケットのように飛んでいきます。

これは、圧力比(風船の内側と外側の圧力差)が大きいからですね。
圧縮機内では、圧力比が大きいと、冷媒漏れが生じる量が多くなるわけです。
このような理由から、圧力比が大きくなると吸込み蒸気量が低下し、体積効率が低下していきます。
最後に
体積効率の記事を基礎編と応用編に分けて解説しました。
この2つの記事を両方理解できれば、もう体積効率の概念は完璧です。
圧縮機には他にも色々な効率(断熱効率、機械効率)がありますので、こちらも覚えていくとさらに圧縮機についての理解が深まると思います。
お役にたてば幸いです。
