ファニングの式｜ダルシーワイスバッハと比較｜ムーディ線図の使い方

流体の圧力損失ΔPを計算するファニングの式を紹介します。

ファニングの式は、管内を流れる乱流状態の流体の圧力損失を表す式です。

実際の流体の圧力損失がどの程度かを見積もりたい場合、ファニングの式が必要になりますので、参考にしてください。

ファニングの式は流体の力の損失分

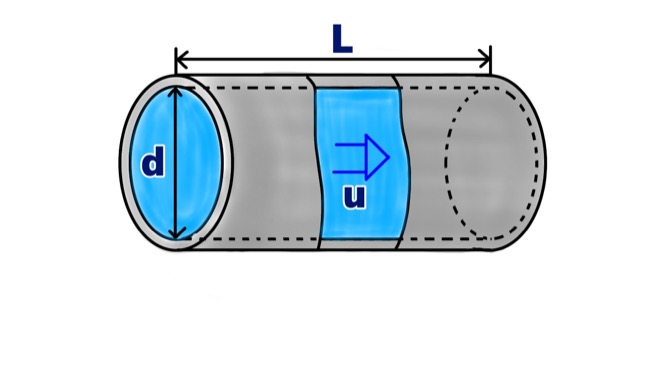
上の絵のように、ある流体が直径dの中を乱流状態で移動するとき、圧力損失ΔPは以下の式で表されます。

$$ \varDelta P＝4 f \frac{\rho u^2}{2} \frac{L}{d}{\tag{1}}$$

ρ：密度\([kg/m^3]\)
f ：摩擦損失係数

これがファニングの式です。

具体的な使用例としては、ポンプの揚程を計算するとき、直管の圧力損失を計算するのに使用されます。

また、イメージでわかりやすくすると、ファニングの式というのは、流体の力の損失分、ということができます。

ファニングの式の導出

流体がもつ力の損失分である、という理由をわかりやすく解説します。

まず、次の図のような配管内に流れる流体の圧力損失ΔPについて考えます。

距離Lの間で圧力が\(P_1\)から\(P_2\)へ減少したとすると、このときの力の損失\(F_1\)は

$$ F_1=\frac{\pi d^2}{4} (P_1-P_2)=\frac{\pi d^2}{4} \varDelta P{\tag{2}}$$

 

で表されます。

 

次に、この流体は管の壁面と摩擦によって力を消耗していきます。

 

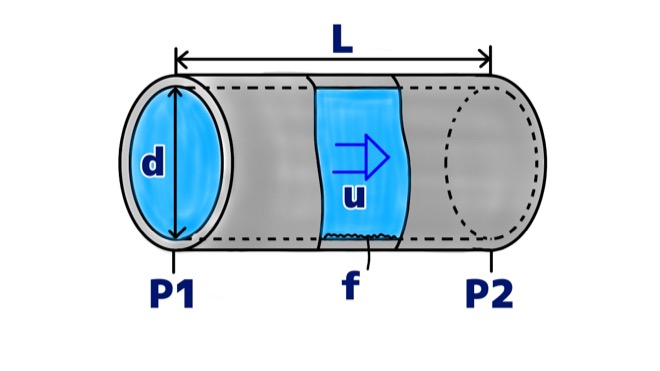
この時の摩擦損失係数をfとすると、壁面との力の損失分\(F_2\)は

$$ F_2＝f \cdot (\pi dL) \cdot \frac{1}{2}\rho u^2 {\tag{3}} $$

流体が壁面に及ぼす力F2によって、圧力は減少し、力の損失\(F_1\)と等しいので

$$ F_1=F_2 \tag{4} $$

となり、この式をΔPについて解いてあげれば、ファニングの式を導出することができます。

流体の運動エネルギーに対しての掛け算/割り算

ファニングの式は、圧力損失について解かれていますが、運動エネルギー\(\frac{1}{2} \rho u^2 \)に対して、他のパラメータである距離Lが掛け算、直径dが割り算してあります。

なので、

と考えてファニングの式を見ると、イメージしやすいです。

以下では、ファニングの式において、圧力損失の増減させる距離L、直径dについて考えてみます。

 

距離Lが長くなると圧力損失は大きくなる

これはイメージしやすいかと思います。
上の絵のように、最初に圧力P1で左から流れていた流体が、同じ直径の管に入ったとします。
下の管の方が長いので、その分だけ管との間で摩擦が生じて圧力が落ちていくのがイメージできるかと思います。
このとき、

$$ P_1 \gt P_2 \gt P_3 {\tag{5}} $$

となります。

距離L1では圧力損失はP1-P2分だけですが、L2まで進むとP1-P3となり、圧力損失は大きくなります。

長い配管の中をずっと流れていると、管との摩擦でエネルギーをロスしていくのは当たり前ですね。
僕らも、長い道のりを歩けば疲れてエネルギーをロスしていきます。

なので、距離のパラメータLは掛け算され、Lが大きいほど圧力損失ΔPは大きくなります。

直径dが大きくなると圧力損失は小さくなる

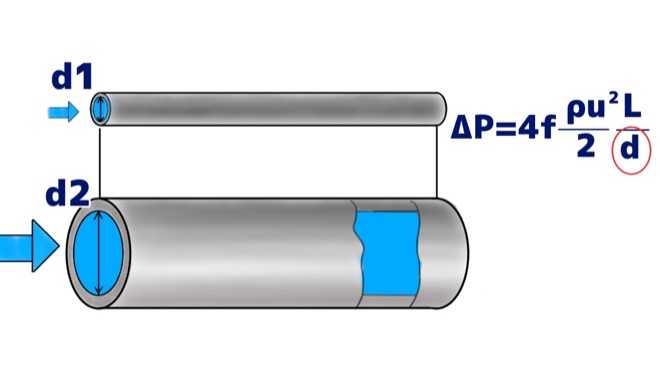
これもイメージしやすいと思います。

細い管と太い管、流体を流す時にどちらがスムーズに流れていくでしょう。

もちろん太い管ですよね。

僕らも、狭い道を歩くより、広い道を歩いた方がスムーズにロスなく歩いていくことができます。これと同じです。

 

なので、管の直径のパラメータdは、式の分母側（割り算側）にあり、dが大きいほど圧力損失ΔPは小さくなります。

 

距離Lと管の直径dでの圧力損失のまとめ

以上の内容を表にまとめると次のようになります。

	値	圧力損失ΔP
長さＬ	長い	大きい
直径d	大きい	小さい

このように、流れる距離Lが長くなるほど圧力損失は大きくなり、直径dが大きくなるほど小さくなります。

 

ファニングの式の使用条件【円管・乱流】

ファニングの式は、使用する時には条件があります。

上記でも触れていますが、以下のような条件があります。

もしも管の断面が円形でない場合には、直径Dの代わりに相当直径Deを用います。

また、乱流でなく層流の場合には、ハーゲンポアズイユの式を用いて計算します。

ここに注意してください。

 

ダルシーワイスバッハの式との違い

機械工学の分野では、ダルシーワイスバッハの式というものが存在します。

こちらもファニングの式と同じで、円管内の圧力損失の式です。

ダルシーワイスバッハの式における圧力損失を\(ΔP_{D-W}\)とすると

$$ \varDelta P_{D-W}=\lambda \frac{\rho u^2}{2}\frac{L}{d} \tag{6} $$

これを(1)式のファニングの式と比較すると、

$$\lambda＝4f \tag{7}$$

となります。

この時、本記事ではλとfを次のように定義しています。

名前が違うだけで、4倍大きいか小さいかだけの同じ意味の係数です。

 

ムーディ線図

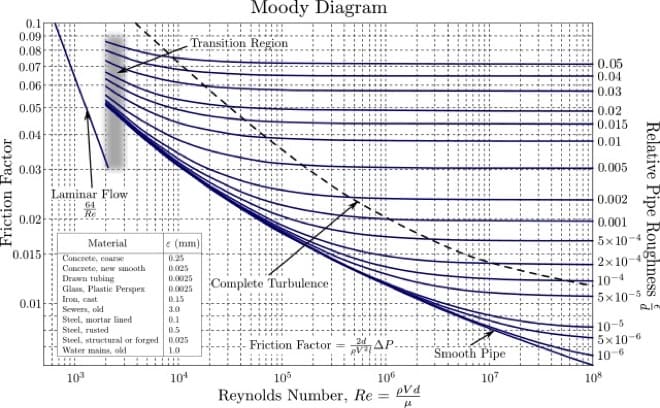
実際の流れに対してファニングの式を適用する際、摩擦係数fをどのように設定すればよいかが悩むところです。

そんな時は、上記のようなムーディ線図という表を使用して、摩擦損失係数を決定します。

 

ムーディ線図とは、横軸にRe数、縦軸の左側に管摩擦係数λ、右側に相対粗さ\(\frac{\epsilon}{d}\)で表され、管摩擦係数fを求めることができるようになっている線図です。

 

ファニングの式を用いる場合は、λ＝4fの式で置き換えて計算する必要があります。

このムーディ線図の使い方ですが、実際の例を取って解説します。

 

摩擦損失係数fの計算例

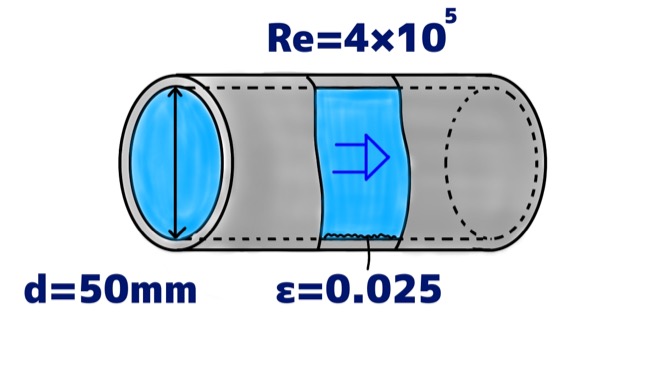
以下のような円管に流れる流体の管摩擦係数λをムーディ線図より求め、最終的に摩擦損失係数fを導出します。

この時、相対粗さは\(\frac{\epsilon}{d}\)なので、\(\frac{\epsilon}{d}\)=\(\frac{0.025}{50}\)≒\(5 \times 10^{-4}\) と計算できます。

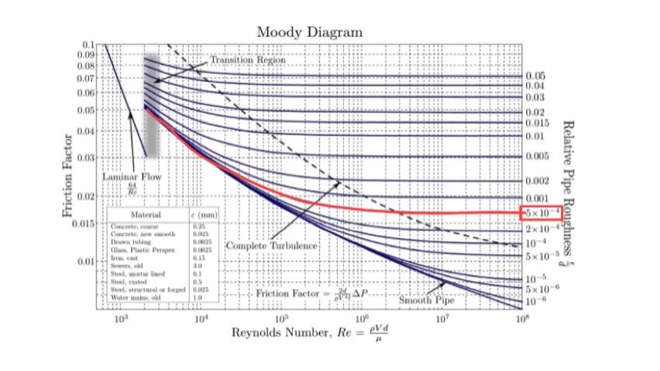
ムーディ線図では、上の図の赤い線が\(5 \times 10^{-4}\)にあたる線になります。

次に、Re数が\(4 \times 10^5\)なので、そこに線を引くと次のようになります。

この交わった点を左に伸ばしていった先が管摩擦係数λとなり、ここでは\(\lambda\)=0.019になりました。

最後に、(7)式より、摩擦損失係数fは\(f=\frac{\lambda}{4} = \frac{0.019}{4} \fallingdotseq 4.8 \times 10^{-3} \)と求められます。

 

このようにして、上記のような条件がわかれば、ムーディ線図から摩擦損失係数fを導出し、実際の圧力損失ΔPを算出することができます。

 

まとめ

今回は以上になります。

ファニングの式は実際の計算にも使える便利な式ですが、乱流の場合に使用され、層流ではハーゲンポアズイユの式を使用することに注意してください。

また、ムーディ線図の左縦軸はλであり、これはダルシーワイスバッハの式の管摩擦係数にあたるので、(7)式を使って変換してあげることが大事です。

以上、お役にたてば幸いです。